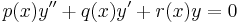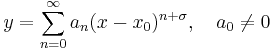Lazarus Fuchs

Lazarus Fuchs
Lazarus Immanuel Fuchs (1833–1902)
Born	May 5, 1833(1833-05-05) Mosina, Prussia
Died	April 26, 1902(1902-04-26) (aged 68) Berlin, German Empire
Residence	Germany
Nationality	German
Institutions	University of Greifswald University of Heidelberg University of Berlin University of Göttingen
Alma mater	University of Berlin
Doctoral advisor	Karl Weierstraß
Doctoral students	Gerhard Hessenberg Edmund Landau Issai Schur Theodor Vahlen Ernst Zermelo
Known for	Fuchsian groups Picard–Fuchs equation Fuchs's theorem
Influences	Ernst Kummer
Influenced	Jules Henri Poincaré Marie Ennemond Camille Jordan Felix Christian Klein

Lazarus Immanuel Fuchs (5 May 1833 – 26 April 1902) was a German mathematician who contributed important research in the field of linear differential equations. He was born in Mosina (located in Grand Duchy of Poznań) and died in Berlin, Germany.

He is the eponym of Fuchsian groups and functions, and the Picard–Fuchs equation; Fuchsian differential equations are those with regular singularities. Fuchs is also known for Fuchs's theorem which states that if x₀ is a regular singular point then the differential equation

$p(x)y''%2Bq(x)y'%2Br(x)y=0\,$

has at least one solution of the form

$y=\sum_{n=0}^\infty a_n(x-x_0)^{n%2B\sigma},\quad a_0\ne0\,$

for some σ to be determined. In some cases, there will be two linearly independent solutions of that form.

Selected works

Über Funktionen zweier Variabeln, welche durch Umkehrung der Integrale zweier gegebener Funktionen entstehen, Göttingen 1881.
Zur Theorie der linearen Differentialgleichungen, Berlin 1901.
Gesammelte Werke, Hrsg. von Richard Fuchs und Ludwig Schlesinger. 3 Bde. Berlin 1904–1909.